Kampfkrafttheorie

Meine Dissertation „Kampfkrafttheorie“ beschäftigt sich mit der Berechnung der Kampfkraft von Armeen in Computerspielen der alten Schule, insbesondere einfachere Onlinespiele.

Die Kampfkrafttheorie ist für Spieler und Entwickler gleichermaßen wichtig.

Der Computerspieler hat den Wunsch nach der stärksten Armee. Diese Theorie bie- tet Formeln, mit dem der Kampf simuliert werden kann. Durch Auswerten der stärksten Einheiten kann die Beste gefunden werden, ohne vorher testen zu müssen. Mit den Optimierungsformeln kann der Spieler die beste Armee zusammenstellen.

Der Spieleentwickler hat den Wunsch nach einem erfolgreichen Spiel. Ein Teil zum Erfolg stellt die Balance dar. Damit das Spiel Spaß macht, müssen die verfügbaren Einheiten nicht nur vielfältig sein, sondern auch gleichberechtigt sein. Für das Ausbalancieren der Einheiten ist die Kampfkrafttheorie notwendig und wesentlich effizienter als zufallsgestörtes Austesten. Der Spieleentwickler kann so verhindern, dass es ein oder zwei Supereinheiten gibt, die alles können. Mit der Kampfkrafttheorie kann er für Vielfalt sorgen und anhand der Optimierungsformeln sogar Einheitenkombinationen genauer ausbalancieren.

Einheiten

Der einfache Kampf

K= f·L·A·N²

Beispiel: Es kämpfen 20 Reiter mit 12 Angriff und 150 Leben gegen 15 Ritter, die 15 Angriff und 180 Leben haben. Die Ritter haben die besseren Werte, sind aber in der Unterzahl. Wer gewinnt?

Lösung

K= f·L·A·N²

K= 0,8·150·12·20²= 576000al

geK= 0,8·180·15·15²= 486000al

Die Reiter werden gewinnen.

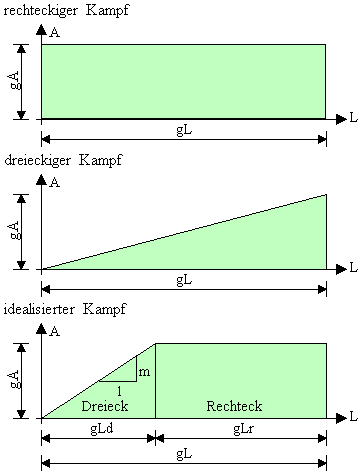
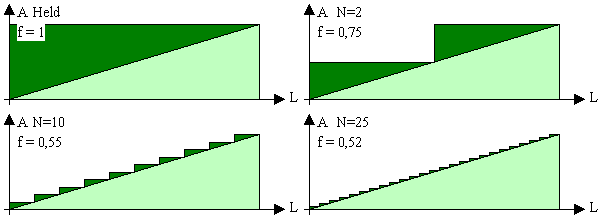
Die Zweiteilung des Kampfes und der Kampfbeiwert

Der Kampfbeiwert f beschreibt die Art und Weise des Kampfverlaufes und beantwortet die Wie-Frage. Es gibt 2 Extremformen des Kampfes: rechteckig und dreieckig

Bei der rechteckigen Kampfweise ist

f= fr =1

Das bedeutet, dass alle Einheiten bis 1 Leben kämpfen und dann bei einem einzigen Schuss alle mit einmal besiegt werden. Dies ist in den meisten Spielen ohne weiteres nicht möglich. Helden kämpfen alleine rechteckig.

Bei der dreieckigen Kampfweise ist

f= fd=0,5

Das bedeutet, dass der Gegner sich immer eine Einheit raussucht und sie abschießt. Erst dann schießt er auf die nächste. Dies schwächt enorm die Kampfkraft. Diese Kampfweise ist möglich, wenn der Gegner solch starke Waffen hat, sodass mit jedem Schuss eine Einheit zerstört wird.

Bei der tatsächlichen Kampfweise liegt f genau dazwischen. 0,5<f<1. Für einheitliche Flotten kann der Kampfbeiwert mit 0,8 geschätzt werden. Der Kampf wird in dreieckig und rechteckig unterteilt.

Dargestellt ist das Kampfverlaufsdiagramm. Die Zeit verläuft von rechts nach links. Der Kampf beginnt also nicht im Ursprung, sondern oben rechts. Der Ursprung ist das Ende des Kampfes, bei der die letzte Einheit fällt. Der Kampfbeiwert ist das Verhältnis aus tatsächlichen Kampf zum rechteckigen Kampf.

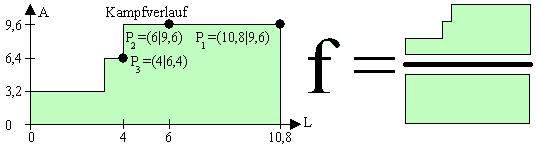
Die Formel für den Kampfbeiwert ohne Streuung lautet:

fu= 1-(2·Lu-1)!/(Lu!·(Lu-1)!)·((1-1/N)/(0,5·4^Lu))

Kampfkraft von beschädigten Flotten

Besiegt man eine Armee, so hat die eigene Armee noch eine Restkampfkraft. Diese erhält man, wenn man von der eigenen Kampfkraft die gegnerische Kampfkraft subtrahiert.

(Rest)K=K-geK

Mit diesen Formeln wird berechnet, wie viel Leben die Einheiten nach dem Kampf noch haben. Wenn die gegnerische Kampfkraft kleiner ist als die eigene rechteckige Kampfkraft

K=(2·f-1)·gA·gL, dann gilt:

gL neu= gL- geK/ gA  sonst

gL neu= ((2-2·f)·L·2·(K-geK)/A)^0,5

Bauteiloptimierungsformel

In einigen Spielen kann der Spieler seine Armee mit Gegenständen ausrüsten. Z.B. kann ein Schlachtraumschiff mit vielen Kanonen, Abwehrschilden und anderen Bauteilen ausgestattet sein. Der Spieler kann sich seine Raumschiffe nach seinem Geschmack konstruieren, ob diese nun viel transportieren können, ob diese schnell, schwach und weitsichtig sind oder langsam und stark. Wenn die Schlachtschiffe dafür konstruiert werden, um möglichst stark zu sein, bietet die Bauteiloptimierungsformel die ultimative Lösung. Die Kampfkraft wird umso größer, je mehr Waffen und Panzerungen man einbaut. Doch der Platz im Schiff ist begrenzt. Je mehr Panzerungen man einbaut, desto weniger Waffen können eingebaut werden. Das richtige Verhältnis aus Waffen und Panzerungen muss gefunden werden.

Die Bauteiloptimierungsformel lautet:

j= (W-Wj·L0/Lj + A0·Wi/Ai)/(2·Wj)

mit

i= Anzahl der Waffen

j= Anzahl der Panzerungen

Wi= Rohstoffkosten pro Waffe

Wj= Rohstoffkosten pro Panzerung

Ai= Angriff der Waffe

Lj= Leben der Panzerung

A0= Angriff der sonstigen Bauteile

L0= Leben der sonstigen Bauteile

W= der begrenzende Rohstoff

Überschaden

Wenn ein Soldat besiegt wird, geht Schaden verloren. Z.B. ein Ritter hält 2,3 Attacken eines Drachen aus. Mit dem dritten Treffer stirbt der Ritter, aber 0,7 Treffer sind zum Besiegen nicht notwendig. Dieser Schaden kann auf die Leben gutgeschrieben werden und heißt Überschaden U. Ganz extrem wird es, wenn mit Kanonen auf Spatzen geschossen wird. Die Spatzen halten so viel aus, wie die Kanone an Schaden anrichtet. Der Überschaden erhöht die Kampfkraft. Damit die Armee diese Lebensgewinne nutzen kann, muss sie jedoch Einheiten verlieren. Kompliziert wird es, wenn man Streuung des Schadens berücksichtigt.

Mit der Überschadensformel kann der Überschaden berechnet werden. Der Überschaden wird zu den Leben der Einheiten hinzuaddiert.

Lu= L+U

Die zusätzlichen Leben wirken aber erst, wenn Einheiten ausscheiden. Das heißt, dass die Armee in der rechteckigen Kampfweise nicht davon profitiert. Der dreieckige Teil wird also verlängert.

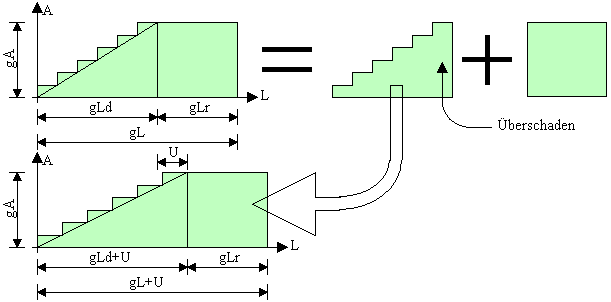
Da der Überschaden nur im dreieckigen Kampf hilft, sinkt der Kampfbeiwert auf fu.

K= fu·Lu·A·N²

Die Formel für den Überschaden lautet:

Function Uschaden(ByVal L As Double, ByVal d As Double) As Double

Dim HV#, T2#, L0#, L1#, minT#, maxT#, Fak#, Fak1#

Dim i%, j%, Q%, vz%, Stutzen As Integer

HV = Int(L) * (1 + d) - L

T2 = L - (1 + Int(L)) * (1 - d)

If HV < T2 Then HV = T2

If HV <= 0.1 ^ 10 Then

 Uschaden = 1 - L + Int(L)

 If L = Int(L) Then Uschaden = Uschaden - 1

Else

 minT = Int(L / (1 + d)) + 1

 If d >= 1 Then maxT = 40 Else maxT = L / (1 - d)

 If maxT > 40 Then maxT = 40

 If maxT <> Int(maxT) Then maxT = Int(maxT) + 1

 Q = maxT - 1: Fak = 1: Uschaden = 1

 For i = 1 To Q

  L0 = (L - i * (1 - d)) / (2 * d)

  Fak = Fak * i

  If i < minT Then

   HV = 1

   Else

   Stutzen = Int(L0): HV = 0: Fak1 = Fak

   vz = -1

   For j = 0 To Stutzen

    If vz = -1 Then vz = 1 Else vz = -1

    HV = HV + vz * (L0 - j) ^ i / Fak1

    Fak1 = Fak1 * (j + 1) / (i - j)

   Next

  End If

  Uschaden = Uschaden + HV

 Next

 Uschaden = Uschaden - L

End If

End Function

und sieht im Diagramm so aus:

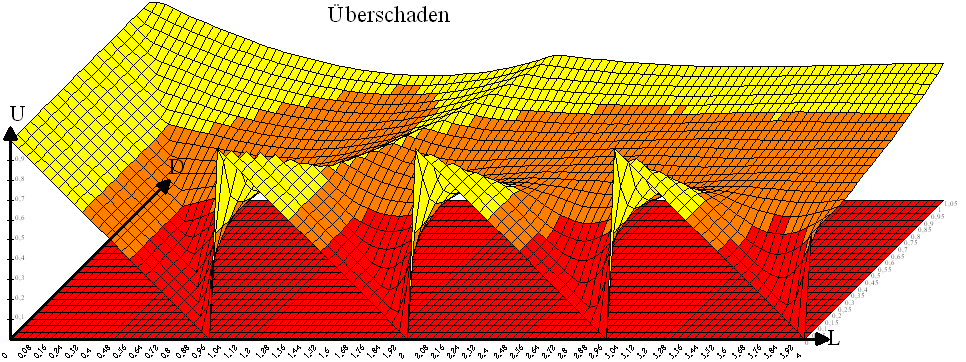
getreppter dreieckiger Kampf

Vereinfachend wurde der Kampf in rechteckig und dreieckig aufgeteilt. Der Kampfbeiwert bestimmt dabei, wie groß das Rechteck davon ist. Bei einem Kampfbeiwert von 0,5 ist der Kampfverlauf dreieckig. Bei dieser Kampfweise wird eine Einheit nach der anderen abgeschossen. Zeichnet man diesen Kampfverlauf genauer auf, so sitzt zusätzlich auf dem Dreieck noch eine Treppe.

fd= 0,5+1/(2·N)

Genauer Kampfverlauf

Vereinfachend wird der Kampf in dreieckig und rechteckig unterteilt. Für genauere Berechnungen bietet dieses Kapitel ein genaueres Kampfmodell. Wie im vereinfachten Modell wird der tatsächliche Kampfverlauf durch eine flächengleiche geometrische Figur nachgebildet. Der Kampfverlauf unterteilt sich in einem rechteckigen und einem gekrümmten Bereich. Da die Steigung des gekrümmten Bereiches mit zunehmender Länge gegen 0 geht, wird dieser durch eine Hyperbel angenähert.

K/A= 0,5·gLd+ geA·m·c·gLd-geA²·m·c²·ln(gLd/geA+c)+geA²·m·c²·ln(c)+(gL-gLd)·N

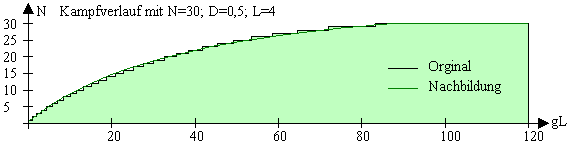
Der genaue Kampfverlauf benötigt die Leben des letzten überlebenden

Zusammenfassung

Für Überschaden, Leben des letzen Überlebenden und Kampfbeiwert gibt es Näherungsformeln:

Überschaden

u= (Abs(2·L-2·Int(L)-1)^(1+0,8/(D·L))·Sgn(2·L-2·Int(L)-1)-(2·L-2·Int(L)-1))/2+0,5+ D²/6-( (D·(2-D)·0,41·Sin(L·2·π)))/(L²+1,2)

Leben des letzen Überlebenden

Function Letzter(ByVal N As Integer, ByVal L As Double, ByVal d As Double) As Double

Dim Lebenreduktion As Double

Dim Term As Double

If L <= (1 - d) Or N = 1 Then

 Letzter = L

 Else

 Term = 2 * L - 2 * Int(L) – 1

 If d = 0 Then

    Lebenreduktion = -Term / 2

    If L - Int(L) = 0 Then Lebenreduktion = Lebenreduktion – 1

   ElseIf L - Int(L) = 0 Then

    Lebenreduktion = 0

   Else

    Lebenreduktion = 0.5 * Sgn(Term) * Abs(Term) ^ (1 + 0.1/(d^2*L)) - Term / 2

 End If

 L = L + Lebenreduktion

 Letzter = 0.8 * L ^ 0.48/N ^ 0.146 – Lebenreduktion

 Letzter = Letzter - (0.9 + 0.25*d) * (0.0067 * L ^ 2

 Letzter = Letzter - 0.5 * L + 0.18) / N^ 2 + 0.085 * (d - 0.5) * Log(L)

 Letzter = Letzter + 0.2 * (d - 0.5) ^ 2 - 0.001 * (d = 0) * N

 Letzter = Letzter - 0.15*d*(1-0.3*Log(N))/(1+1.5*L^2)

End If

End Function

Kampfbeiwert

fu = 1,021-2·(1-0,5/(2·N))·(1+0,15·d)·(0,2-0,05·Log(L+U))+0,21/N + 0,24/L/N2-0,0001· (21·L+580/L)-0,006·L/N

Rechenbeispiel: Eine große Schlacht

20 Panzer kämpfen gegen eine Infanterie, die mit Panzerfäusten ausgestattet ist. Ein Panzer hat 1200HP und eine Angriff von 120 und schießt 1,5 mal pro Sekunde. Die 60 Soldaten halten jeweils 200HP aus und die Panzerfäuste verursachen einen Schaden von 40 bis 80. Die Nachladezeit beträgt eine Sekunde. Laut dem Spiel ist diese Waffe effektiv gegen Panzer und verursacht doppelten Schaden.

gegeben:

Panzerarmee

N= 20

A= 120

1,5 Schuss pro Sekunde

L= 1200 L

Infanterie

geN= 60

geA= 40 bis 80 & doppelter Schaden gegen Panzer

1 Sekunde Ladezeit

geL= 200 L

Diese Werte müssen umgerechnet werden.

A= 120·1,5 = 180 a

geA = (40+80)/2·doppelter Schaden gegen Panzer/1 Sekunde Ladezeit

geA= 120 a

Damit haben die Spieldaten diese nutzbaren Werte für die Berechnung ergeben:

Panzerarmee

N= 20

A= 180 a

S= 120 L

L= 1200 L

Infanterie

geN= 60

geA= 120 a

geS= 120 L

geL= 200 L

Wenn man sofort ungefähre Ergebnisse haben will, kann man den Kampfbeiwert mit 0,8 schätzen und in die Kampfkraftgleichung einsetzen.

K= f·L·A·N²= 0,8·1200·180·20²= 69,12 Mal

K= gef·geL·geA·geN²= 0,8·200·120·60²= 69,12 Mal

Die Armeen sind in etwa gleich stark. Es lohnt sich genau zu rechnen.

Zuerst werden Streuung und das Lebenschadenverhältnis benötigt.

D= (120-120)/120=0

geD = (160-120)/120 = 1/3

s = L/geS= 1200/120= 10

ges= geL/S= 200/120= 1,667

Dann wird der Überschaden benötigt

u= Überschaden(s, geD) = Überschaden(10=L, 1/3= D)

geu= Überschaden(ges, D) = Überschaden(1,667=L, 0=D)

Zuerst wird der Überschaden der Infanterie berechnet

1. u= Überschaden(1,667=L; 0=D)
2. Trivialprüfung
   Int(L)·(1+D)-L = Int(1,667)·(1+0)-1,667 = 1·0-1,667 = -0,667
   L-(1+Int(L))·(1-D) = 1,667-(1+Int(1,667))·(1-0) = 1,667- (1+1)·1= -0,333
3. Da beide Werte unter 0 sind, wird der Überschaden mit der Trivialformel berechnet (und der Kampfbeiwert mit der exakten Formel). Für D=0 ist die Prüfung immer bestanden.
   U=1-L+Int(L)= 1-1,667+1 = 0,333
4. U= 0,333 L/a

Dann wird der Überschaden der Panzerarmee berechnet

1. u= Überschaden(ges;D)
   u= Überschaden(10=L; 0,333=d)
2. Trivialprüfung
   Int(L)·(1+D)-L = Int(10)·(1+0,333)-10= 3,333
   L-(1+Int(L))·(1-D) = 10-(1+Int(10))·(1-0,333)= 2,666
3. Da mindestens eine der Bedingungen nicht erfüllt ist, muss der Überschaden mit dem Hauptteil berechnet werden und der Kampfbeiwert mit der Näherungsformel.
4. Hilfsterm berechnen
   Term = 2· L - 2 · Int(L) - 1= 2·10-2·Int(10)-1= -1
5. Hauptfunxion berechnen
   HV = Abs(Term)^(1+0,8/(D·L))·Sgn(Term)-Term/2+0,5
   HV= 1^(1+0,8/(0,333·10))·(-1)-(-1)/2+0,5= 0,5
6. Korrekturterme berechnen
   Da L > 0,5 ist, muss der lange Term berüchsichtigt warden
   T2= D²/6-( (D·(2-D)·0,41·Sin(L·2·π)))/(L²+1,2)
   T2= 0,333²/6-(0,333·(2-0,333)·0,41·Sin(10·2·π))/(10²+1,2)
   T2= 0,0185
7. U= 0,5+0,0185= 0,5185 L/a

Das Überschadenverhältnis wird in einen Überschaden umgerechnet und zu den Leben hinzuaddiert.

U= 0,5185·120= 62,22 L

geU= 0,333·120= 40 L

Lu= 1200+62,22= 1262,22 L

geLu= 200+40 = 240 L

Übersicht der Zwischenwerte

Panzerarmee

D= 0

s= 10 L/a

u= 0,5185 L/a

U= 62,22 L

Lu= 1262,22 L

Infanterie

geD= 1/3

ges= 1,667 L/a

geu= 0,333 L/a

geU= 40 L

geLu= 240 L

Als letztes muss noch der Kampfbeiwert berechnet werden.

Es sind folgende Werte in die Formel ein zu setzen:

fu= Kampfbeiwert(s,geD,N,u)

fu= Kampfbeiwert(10=L; 1/3=d; 20=N; 0,5185=U)

gefu= Kampfbeiwert(ges; D; geN; geu)

gefu= Kampfbeiwert(1,667=L; 0=d; 60=N; 0,333=U)

Panzerarmee

Die Prüfung war nicht bestanden und es wird die Näherungsformel verwendet.

fu= 1,021-2·(1+0,15·1/3)·(1-0,5/(2·20))·(0,2-0,05·Log(10+0,5185)) +0,21/20+0,24/10/20²-0,0001·(21·10+580/10)-0,006·10/20

fu= 1,021-2,1·0,9875·0,08234+0,0105+0,0001-0,0268-0,003

fu= 0,831

Infanterie

Der Kampfbeiwert wird mit der absoluten Formel berechnet.

gefu= 1-(2·Lu-1)!/(Lu!·(Lu-1)!)·((1-1/N)/(0,5·4^Lu))

geLu= L+U= 5/3 + 1/3 = 2

gefu= 1-(2·2-1)!/(2!·(2-1)!)·((1-1/60)/(0,5·4²))

gefu= 1-6/(2·1)·(0,98333/(0,5·16))

gefu= 1-3·59/(60·8)

gefu= 0,63125

Die Kampfkraft kann nun berechnet werden

K= fu·Lu·A·N²= 0,831·1262,2·180·20²=75,52 Megaangriffsleben

geK= gefu·geLu·geA·geN²= 0,63125·240·120·60²=65,448 Mal

Die Panzer sind der Infanterie leicht überlegen. Dies liegt vor allem daran, die Panzer einfach den größeren Kampfbeiwert haben.

Die Schlacht wird folgendermaßen ablaufen:

K_Rest= K-geK

K_Rest= 75,52-65,448= 10,072 Mal

Die Panzerarmee hat Verluste, wenn deren rechteckige Kampfkraft kleiner ist als die Kampfkraft der Infanterie.

Kr= (2·f-1)·K

Kr= (2·0,831-1)·75,52= 49,99 Mal

Kr < geK

Dies ist der Fall und die Anzahl der übrigen Panzer wird berechnet

N= ((K-geK)/(A·L·(1-f)))^0,5

N= (10,072/(0,18·1,2622·(1-0,831)))^0,5= 16,19 Panzer

zweiheitlicher Kampf - Armee in 2 Reihen

Besteht eine Armee aus Gruppen, bei denen eine Gruppen die Schüsse einsammelt und die andere Schaden austeilt, so wird die Kampfkraft um den zusätzlichen Term a·e·Le·Aa ergänzt. Solche Armeen werden zweiheitliche Armeen genannt. Ein Beispiel für so einen Fall ist, dass die Armee aus Streitkolbenträgern und Langbogenschützen besteht. Die Streitkolbenträger stehen in der ersten Reihe und werden als erstes abgemetzelt, während die Langbogenschützen solange unbeschadet bleiben. Die Langbogenschützen in der zweiten Reihe können aber die ganze Zeit schießen. Streitkolbenträgern und Langbogenschützen stehen in unterschiedlichen Reihen.

Die Kampfkraft setzt sich aus 3 Teile zusammen: Die beiden Eigenkampfkräfte jeder Gruppe und die Teamwirkung.

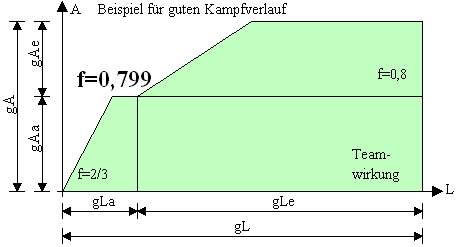
K= fa·La·Aa·a² +fe·Le·Ae·e²+ a·e·Le·Aa

K= Eigenkampfkraft A+Eigenkampfkraft E + Teamterm

dabei sind:

e: Die Anzahl der Einstecker

a: Die Anzahl der Austeiler

Le: Die Leben der Einstecker

La: Die Leben der Austeiler

Ae: Der Angriff der Einstecker

Aa: Der Angriff der Austeiler

fe: Der Kampfbeiwert der Einstecker

fa: Der Kampfbeiwert der Austeiler

We: Der Rohstoffverbrauch der Einstecker

Wa: Der Rohstoffverbrauch der Austeiler

W: Die zur Verfügung stehenden Rohstoffe

Die Vorteile der zweiheitlichen Armee ist, dass die Einheiten sich stärker spezialisieren können, da Angriffsschwächen der Einstecker von den Austeilern übernommen werden und umgekehrt. Bei gut spezialisierten Einheiten wird der Teamterm a·e·Le·Aa groß. Ein weiterer Vorteil sind geringe Reparaturkosten. Es müssen bei gleichem Kampfkraftverbrauch im Verhältnis zu einer einheitlichen Armee weniger Einheiten repariert werden. Den Schaden übernehmen die gepanzerten Einheiten. Sind die Einstecker besiegt, so kann der Rückzug angetreten werden, da die Armee kaum noch Schaden austeilen wird.

Die Nachteile einer zweiheitlichen Flotte sind zum einen die Erfahrung. In Spielen wird meist nur entweder Einstecken oder Austeilen mit Erfahrung vergütet. Eine Reihe bleibt daher fast unerfahren. Der schlimmste Nachteil ist, wenn der Gegner ein in den Rücken fällt. Damit müssen die nackten Austeiler einstecken und die schlecht bewaffneten Einstecker austeilen. Sind die Einstecker Nahkämpfer, so müssen sie sogar warten, bis die Fernkämpfer besiegt sind.

Besteht die zweiheitliche Armee aus 2 Sorten von Einheiten mit ähnlichen Werten so verringert sich die Kampfkraft, als wenn man eine monotone Armee baut. Dies liegt daran, dass zuerst eine Gruppe besiegt wird und so schon viel Angriff fehlt.

Die optimale zweiheitliche Armee

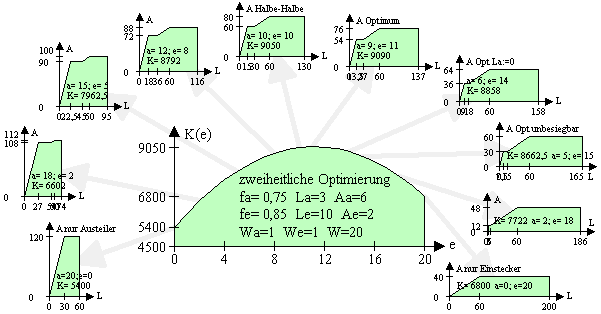
Jedem Kämpfer interessiert vor allem, wie man eine Armee möglichst optimal baut, wie die Armee am stärksten ist. Je mehr Austeiler man hat, desto größer die Kampfkraft. Je mehr Einstecker man hat, desto größer die Kampfkraft. Doch es gibt da eine Grenze, wie viel man bauen kann. Die Anzahl der Einheiten werden meist durch Rohstoffe, Baracken oder Geld begrenzt. Je mehr Austeiler man verwendet, desto weniger Einstecker kann man bauen. Wie viel braucht man nun von welcher Sorte, damit man die effektivste Kombination hat? Das ist ein Extremwertproblem.

Die optimale Anzahl der Einstecker berechnet sich mit

e= (fa·La·Aa·W·We- 0,5·Le·Aa·W·Wa)/(fa·La·Aa·We²+ fe·Le·Ae·Wa²- Le·Aa·We·Wa)

Mischkampf - Verschiedene Gruppen in einer Reihe

Häufig gibt es in den Spielen nur eine Reihe und alle Einheiten, die man gebaut hat, stürzen sich ohne Formation in die Schlacht. Für den Mischkampf gibt es mehrere Modelle.

1. lineare Mischformel
2. nichtlineare Mischformel
3. verbesserte nichtlineare Mischformel
4. Simulation

Die Modelle haben ihre Vor- und Nachteile.

lineares Modell

Beschreibung: Alle Schiffe werden gleich häufig angeschossen. Wie viele Schüsse die einzelnen Gruppen treffen wird zu Anfang über die Anzahl festgelegt.

Vorteile: leicht verständlich, einleuchtend, schnell implementierbar, simple Formeln mit den 4 Grundrechenarten, Diagrammpunkte, Optimierungsformel

Bug:Scheiden Schiffe aus, so wird die Gruppe mit fehlenden Schiffen öfter getroffen.

nichtlineares Modell

Beschreibung:Im Gegensatz zum linearen Modell werden auch alle Schiffe gleich häufig getroffen, wenn Einheiten bereits fehlen.

Vorteile:eine Formel ohne lästige Fallunterscheidungen, Optimierungsformel

Nachteile:riesengroße Formel mit Exponenten, Fehleranfällig beim Abschreiben

verbessertes nichtlineares Modell

Beschreibung:Anstelle eines trapezigen Kampfverlaufes wird der genauere Kampfverlauf eingebaut

Vorteil:präziseres Ergebnis

Nachteile:Es gibt keine Formel. Wenn diese doch gefunden wird, dann ist sie noch länger, komplizierter und unhandbarer als die nichtlineare Mischformel.

Simulation

Beschreibung:Es werden unzählig viele Kämpfe ausgewertet wie in dem Makro Massenschlacht

Vorteil:präzises Ergebnis

Nachteil:Das ist keine Formel!

Die lineare Mischformel lautet:

K= fa·La·(a+b)·a·Aa+ (a·La+ fb·b·Lb)·b·Ab für (La < Lbr) sonst

K= fa·La·(a+b)·a·Aa+(a+b)·(La-(2·fb-1)·Lb)·0,5·(b·Ab+(Ab·b·(Lb-La))/(Lb·(2-2·fb)))+ (2·fb-1)·Lb·(a+b)·b·Ab+ Ab·(Lb-La)²·b²/(Lb·(2-2·fb)·2)

Die nichtlineare Mischformel in dekomprimierter Schreibweise lautet:

K=La*(2*fa-1)*(Na+Nb)*(Nb*Ab+Na*Aa)+Nb*Ab*( Lb*(2*fb-1)*Nb- La*(2*fa-1)*Nb+Na* La*(2-2*fa)- La*(2-2*fa)*Na*e^((La*(2*fa-1)-Lb*(2*fb-1))/La*(2-2*fa)))+Nb*Aa* La*(2-2*fa)*(Na- Na*e^((La*(2*fa-1)-Lb*(2*fb-1))/La*(2-2*fa)))+ Aa*Na^2*La*(2-2*fa)*0,5+Ab*Nb^2* Lb*(2-2*fb)/2+ (Ab+Aa)* Na*e^((La*(2*fa-1)-Lb*(2*fb-1))/La*(2-2*fa))*Nb/(1/( Lb*(2-2*fb))+1/ (La*(2-2*fa)))

Dabei sind:

n= Anzahl der Schiffe n= a+b

fa= Kampfbeiwert der Schiffe mit der geringeren Leben

fb= Kampfbeiwert der Schiffe mit der höheren Leben

a oder Na= Anzahl der Schiffe mit der geringeren Leben

b oder Nb= Anzahl der Schiffe mit der höheren Leben

gAa= Gesamtangriff der Schiffe mit der geringeren Leben

gAb= Gesamtangriff der Schiffe mit der höheren Leben

gLa= GesamtLeben der Schiffe mit der geringeren Leben

gLb= GesamtLeben der Schiffe mit der höheren Leben

Aa= Angriff eines der Schiffe mit der geringeren Leben

Ab= Angriff eines der Schiffe mit der höheren Leben

La= Leben eines der Schiffe mit der geringeren Leben

Lb= Leben eines der Schiffe mit der höheren Leben

Natürlich kann man auch Mischarmeen optimieren. Die optimale Anzahl der Gruppe B lautet:

Nb = (La*fa*Aa*Wb*W-0,5*(Aa+Ab)*W*Wa*(La+e^((La*(2*fa-1)-Lb*(2*fb-1))/(La*(2-2*fa)))*(1/(1/(Lb*(2-2*fb))+1/(La*(2-2*fa)))-La*(2-2*fa))))/(La*fa*Aa*Wb^2+Lb*fb*Ab*Wa^2+(Aa+Ab)*Wb*Wa*(e^((La*(2*fa-1)-Lb*(2*fb-1))/(La*(2-2*fa)))*(La*(2-2*fa)-1/(1/(Lb*(2-2*fb))+1/(La*(2-2*fa))))-La))

Rechenbeispiel: die stärkste Einheit finden

Ein neues mittelalterliches Spiel kommt raus. Prachtvolles Design und viel Reklame. Es gibt viele verschiedene Einheiten, Erfahrungspunkte, Ausrüstung und Technologien und verspricht jede Menge Taktik. Als 16/6 Gamer stellt sich ihm die Frage, welche Einheit ist die stärkste?

So geht man vor. Man sucht sich die maßgebenden Highend-Typen raus und berechnet die reinen Kampfkräfte. Dann berechnet man Kombinationen aus denen.

Im Spiel kann man seine Soldaten leicht, mittel und schwer ausrüsten. Bei der leichten Ausrüstung schwingt der Soldat eine beidseitige Axt und verursacht großen Schaden. Ein schwer ausgerüsteter Soldat sticht mit einem kleinen Schwert zu und schützt sich mit einem Turmschild. Die mittlere Ausrüstung besteht aus einem Schild und einem langem Schwert und stellt damit eine gute Balance zwischen Austeilen und Einstecken dar. Die Taktik des Gamers liegt darin, Offensive und Defensive für maximalen Erfolg auf dem Schlachtfeld zu kombinieren. Für Premiumnutzer gibt es noch einen Bogen. Dadurch ergeben sich völlig neue taktische Möglichkeiten.

Im späten Spiel kann man bis zu 40 Soldaten anführen und diese Werte haben die Soldaten:

• Der Bogenschütze verursacht 9 bis 13 Schaden, hält 186 Schaden aus und kostet 360 Gold.
• Die offensiven Axtkämpfer hacken mit 13 bis 21 Schaden zu, können nur 171 Schaden einstecken und kosten je 420 Gold.
• Soldaten mit mittlerer Ausrüstung teilen 10 bis 16 Schaden aus, halten 226 aus und kosten 290 Gold. Die Rüstung mindert den Schaden um 20%. Da dieser Einheitentyp so oft gebaut wird, wird er oft als Normalo bezeichnet. Der Preis wurde später auf 580 erhöht.
• Schwer gepanzerte Soldaten verursachen 8 bis 10 Schaden, stecken 210 Schaden ein und kosten 330 Gold. Die schwere Rüstung mindert den Schaden um 40%. Die Langlebigkeit dieses Typs hat ihn den Namen Deffer eingebracht.

Alle Einheiten attackieren mit gleicher Geschwindigkeit.

Die maximale Anzahl der Soldaten wird durch den Rohstoff „maximale Anzahl der Soldaten“ begrenzt. Auch wenn es trivial ist, jeder Soldat kostet ein Soldat. Dadurch können von jeder Sorte 40 Soldaten ausgebildet werden. Gold gibt es genug im Spiel, sodass das Limit schnell erreicht ist.

Der Rüstungsbonus wird in zusätzliche Leben umgerechnet. Beispiel für die defensiven Einheiten:

L= 210/0,6= 350 L

Der Angriff ist die Mitte zwischen maximalen und minimalen Schaden.

Für jeden Soldatentyp müssen nun Überschaden und Kampfbeiwert berechnet werden. Die Berechnung dieser Werte ist sehr lang. Die Berechnung ist hier nicht möglich, weil der Gegner nicht bekannt ist. Deshalb kann man diese Werte nur schätzen. Ein Überschaden wird hier jetzt nicht berücksichtigt. Schaut man sich das Lebenschadenverhältnis an, dann ist es in einem Kampf zwischen offensiven Einheiten bei 10. 10 ist ein großer Wert. Für Kämpfe zwischen andere Typen ist das Lebenschadenverhältnis noch größer. Deshalb wird der Kampfbeiwert nicht mit 0,8, sondern größer geschätzt.

Nun können auch schon die reinen Kampfkräfte berechnet werden.

K= f·L·A·N²

K= 0,86·186·11·40²= 2815296 (Bogenschützen)

K= 0,85·171·17·40²= 3953520 (Axtkämpfer)

K= 0,88·282,5·13·40²= 5170880 (Normalo)

K= 0,9·350·9·40²= 4536000 (Deffer)

Zusammenfassung

Die Kampfkräfte sehen schon man nicht ausgewogen aus. Die Normalos sind stark. Der kostenpflichtige Bogenschütze ist alleine sehr schwach, verspricht in Kombination mit einer anderen Einheit aber sehr sinnvoll zu sein. Reine Kampfkräfte dürfen fehlbalanciert sein, um Mischarmeen für das Spiel Interessanter zu machen.

Anschließend werden die Kombinationen aus 2 Typen berechnet. Es gibt insgesamt 6 Möglichkeiten. Bei den Möglichkeiten muss man beachten, dass man die richtige Formel verwendet. Kämpfen beide Gruppen in einer Reihe, dann nimmt man die Mischformel. Gibt es 2 Reihen, dann nimmt man die zweiheitliche Formel. Bogenschützen sind Fernkämpfer und können daher eine zweite Reihe bilden.

Möglichkeiten:

1. Axtkämpfer + Normalos (Mischformel)
2. Axtkämpfer + Deffer (Mischformel)
3. Normalos + Deffer (Mischformel)
4. Axtkämpfer + Bogenschützen (zweiheitliche Formel)
5. Normalos + Bogenschützen (zweiheitliche Formel)
6. Deffer + Bogenschützen (zweiheitliche Formel)

Offensive Soldaten mit defensiven zu kombinieren scheint sehr sinnvoll zu sein.

Auch die Bogenschützen hinter einer defensiven Reihe zu stellen hat den Anschein richtig Sinn zu machen.

Ob dies auch tatsächlich so ist, zeigen die Optimierungsformeln. Aber zuerst werden die Kampfkräfte für Halbe-Halbe berechnet.

erste Möglichkeit: 20 offensive Axtkämpfer mit 20 Normalos

Die Soldaten mit mehr Leben erhalten den Buchstabe b und es muss überprüft werden, ob La < Lbr.

b=20                  a=20

Lb= 282,5          La=171

Ab= 13               Aa= 17

fb= 0,88             fa=0,85

Lbr= (2·fb-1)·Lb = (2·0,88-1)·282,5

Lbr= 214,7

Da die rechteckigen Leben der Gruppe b größer sind als die Leben der Gruppe a, so ist die kurze Mischformel anzuwenden.

K= fa·La·n·gAa+ (gLa+ fb·gLb)·gAb

K1= 0,85·171·(20+20)·20·17+(20·171+0,88·20·282,5)·20·13

K1= 4158680

zweite Möglichkeit: 20 offensive Axtkämpfer mit 20 Deffer

Da die defensiven Einheiten mehr Leben haben, als die mittleren Soldaten, leuchtet ein, dass hier wieder die kurze Mischformel benutzt wird.

K2= 0,85·171·(20+20)·20·17+(20·171+0,9·20·350)·20·9= 3726360

K2= 3726360

dritte Möglichkeit: 20 Normalos mit 20 Deffer

Die defensiven Einheiten erhalten den Buchstabe B und es muss überprüft werden, ob La < Lbr.

a=20                  b=20

La= 282,5          Lb=350

Aa= 13               Ab= 9

fa= 0,88             fb=0,9

Lbr= (2·fb-1)·Lb = (2·0,9-1)·350

Lbr= 280

Lbd= L-Lbr= 350-280= 70

gAa= 13·20= 260

gAb= 9·20= 180

Da Lbr < La, wird die lange Mischformel verwendet

K= fa·La·n·gAa + n·(La-Lrb)·0,5·(gAb+ gAb·(Lb-La)/Lbd)+Lbr·n·gAb + Ab·(Lb-La)²·b²/(Lbd·2)

K3= 0,88·282,5·40·260+40·(282,5-280)·0,5·(180+180·(350-282,5)/70)+280·40·180+9·(350-282,5)²·20²/(70·2)

K3= 4736279

vierte Möglichkeit: 20 offensive Axtkämpfer mit 20 Bogenschützen

Die Bogenschützen stehen in zweiter Reihe und sind die Austeiler.

K= fa·La·Aa·a² +fe·Le·Ae·e²+ a·e·Le·Aa

K4= 0,86·186·11·20²+0,85·171·17·20²+20·20·171·11

K4= 2444604

fünfte Möglichkeit: 20 Normalos mit 20 Bogenschützen

K5= 0,86·186·11·20²+0,88·282,5·13·20²+20·20·282,5·11

K5= 3239544

sechste Möglichkeit: 20 Deffer mit 20 Bogenschützen

K6= 0,86·186·11·20²+0,9·350·9·20²+20·20·350·11

K6= 3377824

Trägt man die reinen Kampfkräfte und den Zwischenpunkt in einem Optimierungsdiagramm auf und legt eine Parabel durch die 3 Punkte, dann ergibt sich dieses Schreckensbild:

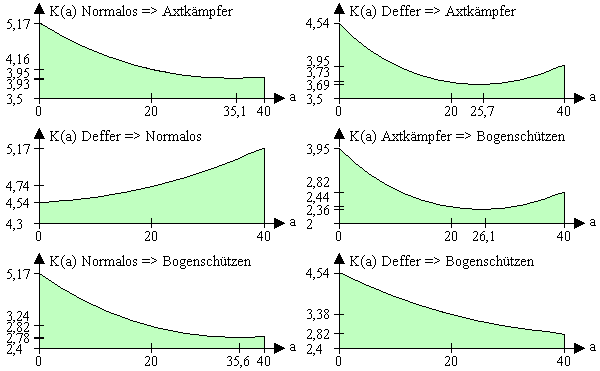
Aufgetragen ist die Kampfkraft (Einheit: Megaangriffsleben) in Abhängigkeit von der Anzahl a. b oder e ist dann die übrige Anzahl des anderen Einheitentyps.

Der üble Verdacht lässt sich durch Auswerten der Optimierungsformeln bestätigen.

Beispielhaft wird jetzt nur die erste und die vierte Möglichkeit die Berechnung dokumentiert. Für die anderen Möglichkeiten erscheint nur das Ergebnis.

1.Moglichkeit

Die Optimierungsformel liefert die Anzahl der Einheiten der Gruppe b

b= (0,5·W·Ab +fa·Aa·W·(0,5-Wb/Wa))/((1-Wb/Wa)·fa·Aa·Wb +Wb·Ab -fb·Lb·Ab·Wa/La)

b= (0,5·40·13+0,85·17·40·(0,5-1/1))/((1-1/1)·0,85·17·1+1·13-0,88·282,5·13·1/171)

b= 4,9157 Normalos

Die Anzahl a wird über die Rohstoffbedingung berechnet

a= (W- Wb·b)/Wa= (40-1·4,9157)/1

a= 35,0843 Axtkämpfer

Das Optimum ist baubar und die Kampfkraft beträgt

K1= 0,85·171·40·35,0843·17+(35,0843·171+0,88·4,9157·282,5)·4,9157·13

K1= 3929142

Die Kampfkraft ist kleiner als die reinen Kampfkräfte und ist damit ein Minimum.

14,3 Deffer +25,7 Axtkämpfer

K2= 3685455 (Minimum)

47,1 Deffer -7,1Normalos

K3= 4521258 (Minimum)

4.Möglichkeit

e= (fa·La·Aa·W·We- 0,5·Le·Aa·W·Wa)/(fa·La·Aa·We²+ fe·Le·Ae·Wa²- Le·Aa·We·Wa)

Da We=1 und Wa=1, wird die Formel erstmal vereinfacht

e= (fa·La·Aa·W- 0,5·Le·Aa·W)/(fa·La·Aa+ fe·Le·Ae- Le·Aa)

e= (0,86·186·11·40-0,5·171·11·40)/(0,86·186·11+0,85·171·17-171·11)

e= 13,9444 Axtkämpfer

a= (W- We·e)/Wa= (40-1·13,9444)/1

a= 26,0556 Bogenschützen

K= fa·La·Aa·a² +fe·Le·Ae·e²+ a·e·Le·Aa

K4= 0,86·186·11·26,0556²+0,85·171·17·13,9444²+26,0556·13,9444·171·11

K4= 2358445

Auch hier handelt es sich um ein Minimum.

4,4Normalos + 35,6 Bogenschützen

K5= 2779321 (Minimum)

-8,8 Deffer+ 48,8 Bogenschützen

K6= 2756479 (Minimum)

Zusammenfassung der Optimierung

Das Spiel ist die reinste Katastrophe. Die Soldaten sind völlig unausgewogen. Jeder Spieler rennt nur mit Normalos rum. Ein monotoner Einheitentyp dominiert das Spiel. Die 16/6 Gamer verschwinden vor Langeweile, die paar 24/7 Zocker haben ihre Freude daran Anfänger zu knechten und die Premiumnutzer fühlen sich total verarscht. Die versprochene Taktik der Bogenschützen geht nach hinten los, da die schwachen Bogenschützen alleine stärker sind als mit Unterstützung. Egal was man kombiniert, es wird nur schlechter. Damit das Spiel Spaß macht, muss beim Kombinieren mindestens irgendwo ein Optimum sein.