Kunstwerke
Mit der Zeit habe ich auch einige Kunstwerke in WMF geschrieben. Diese Art Grafiken zu erzeugen ist eine Alternative zum WMFzerleger. Der WMFzerleger ist sehr unbequem, da man sich über jedes Byte gedanken machen muss, wo man dieses in Excel einträgt. Eine Liniezeichnen mit "LinieZeichnen" geht viel einfacher, hab aber den Nachteil, dass man eine leere Exceltabelle sieht. Was ich für bunte Bildchen nutze, kann man durchaus auch im Berufsalltag gebrauchen. Z.B. eine Exceltabelle, die die passende Grafik dazu maßgetreu generiert.
Alle Grafiken als WMF, wie sie vom Makro erzeugt werden. Die Exceltabelle selbst ist fast leer, da die Grafiken per Code generiert werden.
Kunst.zip
Archivdatei im ZIP Format [3.5 MB]
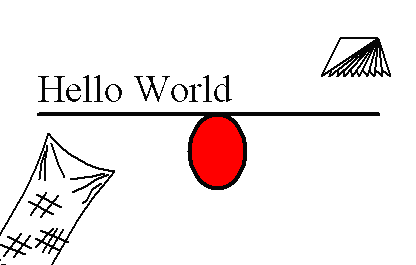
Hello World
Dieses kleine Makro erzeugt diese Grafik
Sub HelloWorld()
Dim Datei$, Text As String
Dim a As Integer
Datei = PinselErstellen(255, 0, 0) & PinselErstellen(255, 255, 255)
Datei = Datei & FüllerErstellen(10, 0, 0, 0) & FüllerErstellen(4, 0, 0, 0)
Datei = Datei & FontErstellen(120, 0)
Datei = Datei & ObjektWählen3(0, 2, 4)
Datei = Datei & LinieZeichnen(100, 300, 1000, 300)
Datei = Datei & EllipseZeichnen(300, 500, 500, 650)
Text = "Hello World"
Datei = Datei & TextZeichnen(Text, 180, 100)
Datei = Datei & ObjektWählen2(1, 3)
For a = 1 To 10
Datei = Datei & DreieckZeichnen(1000, 100, 900, 100, 1050 - 20 * a, 200)
Next
Call DeckchinZeichnen(100, 600, 100, 2.3, 30, 52, "", "03000000", Datei, Datei, Datei, Datei, Datei, Datei, Datei, Datei, Datei, Datei, Text)
Call WMFdateiErstellen("HelloWorld", Datei, 1100, 700, 254)
End Sub
Der Code macht folgendes:
Variablen werden Definiert. Datei ist ein String.
Zunullt wird ein roter Pinsel angelegt und dann wird zuerst ein weißer Pinsel angelegt. Als zweites folgt ein dicker schwarzer Füller und als drittes ein dünner schwarzer Füller. Als viertes wird noch ein waagerechter Font defniert. Die Nummern sind wichtig, denn diese Malobjekte müssen noch ausgewält werden.
Es werden die Objekte 0; 2 und 4 ausgewählt, also der rote Pinsel zum Ausmalen und der dicke Füller zum Umranden und der Font zum Schreiben.
Anschließend folgen einfache geometrische Objekte wie Linie, Ellipse, Text und Dreiecke, die ihre geometrischen Koordinaten haben wollen. Diese Funxionen ergänzen die fehlenden Bytes, damit die Koordinaten zu einem geometrischen Objekt werden und geben den entsprechenden ASCII-Code aus.
Der ASCII-Code wird in der Variablen Datei abgelegt.
Es werden die Objekte 1 und 3 ausgewählt. Der rote Pinsel wird gegen den weißen ausgetauscht und der dicke Füller durch den dünnen Füller.
DeckchinZeichnen ist eine komplexe Funxion, die gleich mehrere geometrische Objekte aufeinmal zeichnet.
WMFdateiErstellen bekommt den String "Datei" und macht daraus ein WMF. Um Nebensächlichkeiten, wie einem korrekten Header, braucht man sich nicht zu kümmern.
fraktale Bäume
Bäume... An Einer Line werden 4 kleinere Linien gesetzt. Unterschreitet die Linie eine Länge, dann erhält sie keine neuen Linien, sondern einen grünen Kreis am Ende. Mit einer Wahrscheinlichkeit von 1% wird statt eines Blattes eine Blüte gesetzt.
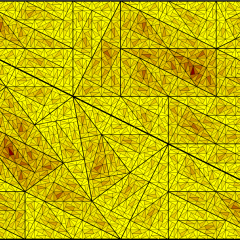
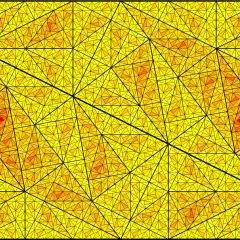
fraktale Dreiecke
Dreiecke... Ein großes Dreieck wird in 5 ähnlich große Dreiecke geteilt. Es gibt 2 Möglichkeiten zum Teilen. Die eine Variante führt zu einem regelmäßigen Muster, die andere zu einem unregelmäßigen.
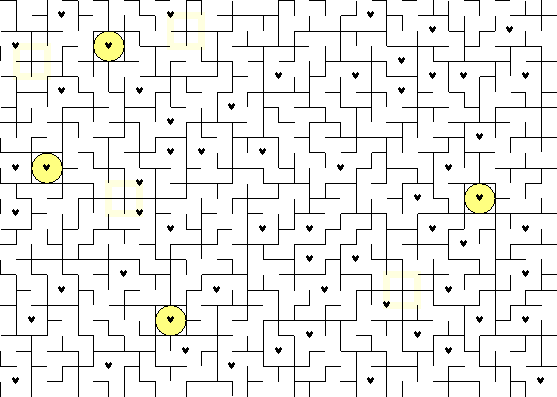
Jfeld
Auf einem kariertem Papier wird bei jedem geraden Quadrat die rechte xoder die linke Seite nachgezeichnet und bei jedem ungeradem Quadrat die obere xoder die untere. Ein Quadrat ist gerade, wenn x+y= gerade ist; alle schwarzen Quadrate beim Schachbrett sind gerade und die ungeraden sind weiß. Dadurch sind maximal 3 Quadrate horizontal oder vertikal verbunden. Die Wände bilden Bereiche. Eine Besonderheit ist, dass in jedem Bereich jenau ein großes Quadrat ist, das mit einem herz markiert wird.
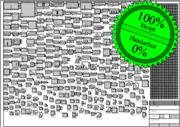
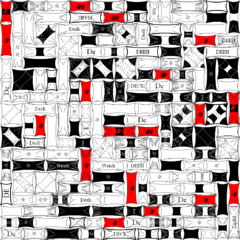
prozedurale Werkstattplanung
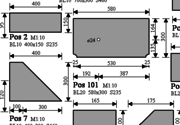
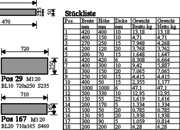
Ein Zufallsgenerator erzeugt 288 Bleche und erstellt daraus einen Einzelteilplan. Jedes Blech kann ein Bohrfeld oder ein Schlitz haben. Zusätzlich kann jedes Blech ein Trapez sein oder ausgerundete Ecken haben. Jedes Blech wird mit seiner Positionsnummer beschriftet und erhält die beiden Gesamtmaßketten. Zusätze wie Bohrfeld/Schlitz und Trapez/Ausrundungsradien erhalten ihre eigene Polymaßkette. Um Platz zu sparen erhalten große Bleche den Maßstab 1:20 und der Maßstab 1:5 schafft den Platz für detailierte Maßketten. Jedes Blech beansprucht mit seinen Maßketten und Text unterschiedlichen Platz auf dem Plan. Ein Fensteranordnungsalgorithmus platziert die Bleche auf dem A0 Plan platzsparend. Platzsparende Methoden sind überlappende Ecken, 2 schmale Bleche statt ein breites in eine Lücke einprüfen, große Bleche zuerst. Zusätzlich wird auf dem A0 Plan eine Stückliste und ein Plankopf generiert. Der Placeable Header des WMF ist auf 254 eingestellt, sodass die Datei die Abmessungen eines A0-Plans hat. 1 Einheit = 0,1mm Papier= 1mm Blech bei M1:10. Da nur ganze Zahlen bis 32767 erlaubt sind, können Blechabmessungen hier keine Nachkommastellen haben. Excel zeichnet den Plan in etwa 3 Sekunden - so schnell geht Werkstattplanung. Für die Praxis sollte man Excel aber nicht in WMF zeichnen lassen, sondern in AutoCAD.
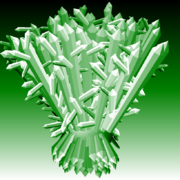
wertvolle Kristalle
Kristalle... in prachtvoller Schönheit. Kleines Programm mit großem Glanz.
Lshape
Auf einem karierten Papier werden L Formen plaziert. Das ganze Papier soll ausgefüllt werden. Es gibt unendlich viele Möglichkeiten, wie man das Papier ausfüllt. Die triviale Möglichkeit ist, dass man aus 2 Ls Rechtecke bildet, mit den man dann ausfüllt. Da es 2 Varianten gibt, das Rechteck zu füllen, beinhaltet das Rechteck 1 Bit an Entropie. Ein L trägt damit ein halbes Bit. Geht das auch mit einem Bit pro L? Untersucht werden verschiedene Möglichkeiten, wie man das Feld parkettieren kann: Rechtecke unterschiedlicher Länge und mit unterschiedlichem Inhalt und wie man sie noch nachträglich verzahnen kann.
Möglichkeiten das Feld mit möglichst hoher Entropie zu füllen.
Lshape.docx
Microsoft Word-Dokument [104.0 KB]
B und K
Bauen Nach Bestell und Krempelladen. Die Seitenansichten dieser Gebäude füllen eine Fläche. Bauen Nach Bestell ist eine Möbelfirma, die von den geldgierigen Katzen Miaunza und Maunzi geführt wird und weitere Katzenanhänger hat. Krempelladen ist ein Laden voller Krempel, der von hufwütigen Elchen namens Elchiuter und Elchameboy verwaltet wird und weitere Katzen und Elche sind in dem Laden.
RöRo Traggerüstsysteme
Traggerüste in verschienensten Varianten, die das Herz höher schlagen lassen. Das Makro WeiRö2 zeichnet Grundriss, Längsschnitt und Jochschnitte vom Traggerüste in AutoCAD. Es wird zwischen RöRo-Traggerüste und Weisetraggerüste unterschieden. Bei einem RöRo-Traggerüst werden die Stützen mit Kopfspindeln und Einzelteilen gezeichnet, während Co.Weise nur einen fetten Strich zeichnet. Dadurch sehen Weisetraggerüste so furchtbar hässlich aus, während die Traggerüste von der RöRo ästhetisch sehr reizvoll sind. Da es hier um Kunst geht, werden die RöRo-Traggerüste wegen ihrer Liebe zum Detail bevorzugt. WeiRö2 zeichnet Längsträger, Jochquerträger, Stützen, Fußträger, Rohrverbände und Anbauteile wie Abspannungen in Grundriss, Längsschnitt und Jochschnitte und beschriftet, kotiert und bemaßt diese.
Es gibt eine genauere Beschreibung zum Thema Traggerüste mit Excel zeichnen.
Fünfecke
Ein Fünfeck mit gleichen Seitenlängen ist durch 2 Winkel eindeutig definiert. 3 Linien der Länge 1 und die beiden Winkel formen eine Polylinie. Ist der Abstand zwischen den Start- und Endpunkt < 2, dann lässt sich das Polygon mit 2 weiteren Linien zweideutig schließen. Ich entschied mich für eine Lösung, da die andere bei gespiegelten Winkeln auftritt. Der Parameter x variiert die Länge der letzten beiden Linien.
Beide Winkel werden von -3,1 bis 3,1 in 0,2 Schritten variiert. Damit entstehen alle erdenklichen 5 Ecke. Ist das Fünfeck ungültig, dann hat es keine graue Füllung, denn es ist ja nur eine Polylinie mit 5 Segmente und kein Polygon.
Ist x=1, dann sind alle Längen gleich. In der Mitte gibt es den Bereich der ungültigen Fünfecke. Interessant ist auch der Fall x=0,5. Dann formen die ungültigen Fünfecke ein großes Sechseck (also keine runde Form), das von Vierecken umrandet ist.
Lateinmuster
Beim trockenen Latteunterricht war ich oft unkonzentriert und malte Pfeile in den Hefter, die an den Seiten abprallen. Ein Kästchen enthält genau 2 sich kreuzende Pfeile. In einem Rechteck wird oben links und unten links ein Pfeil eingeschossen, der sich durch das Rechteck bewegt. Bis zur nächsten Kante bildet es eine Linie aus Pfeile, die in eine Richtung zeigen. An den Seiten prallt der Pfeil ab. Irgendwann trifft der Pfeil auf eine Ecke oder einen Kästchen, das bereits ein Pfeil hat und endet damit. Damit die Pfeile sich kreuzen, muss der zweite Pfeil eingeschossen werden. Hat das Rechteck teilerfremde Abmessungen, dann ist das Lateinmuster komplett. Je großer der größte gemeinsame Teiler, desto mehr Pfeilschüsse werden zum Füllen benötigt. Im Hausaufgabenheft hatte ich noch richtige Pfeile gemalt. Das Muster ist bei Pfeilen schwer zu sehen. Deshalb muss die vordere Pfeilhälfte mit dem Filzer nachgemalt werden oder in WMF wird nur die Linie der Pfeilhälfte ohne Spitze gemalt.
Da die Lateinmuster so vielfältig sind, haben diese mich fasziniert und sie sehen jedesmal anders aus. Selbst bei gleichen Abmessungen gibt es 2 verschiedene.
Zu den Lateinmustern habe ich auch noch eine ausführliche Beschreibung.
Dieses rar-Archiv packte 2,5 mal besser als ZIP und enthält ein voluminöses RTF-Dokument mit alle Lateinmuster von 3x3 bis 52x52. Es sind 5210 Grafiken. 550 Zeilen, die es in sich haben: Die Berechnung des Dokumentes dauerte 10 Minuten. Größte gemeinsame Teiler von mehr als 4 sind nicht enthalten. Bei der zweiten Version habe ich Farben und GgT von 3 und 4 hinzugefügt und duplikate bei GgT 2 ausgefegt.
Lateinmuster2.rar
Komprimierte Archivdatei [6.0 MB]
Bewege 2 Streichhölzer, sodass die Gleichung stimmt
Das klassische Rätsel. Eine falsche Gleichung liegt vor und man soll 1 bis 3 Streichhölzer bewegen, damit sie stimmt. Hier habe ich den Weg rückwärts gemacht. Eine beliebige Gleichung ist gegeben und es werden 2 beliebig Streichhölzer so bewegt, sodass gültige Symbole entstehen. Von den beliebigen Gleichungen kann eine wahre Gleichung gewählt werden und man erhält dan alle veränderten Gleichungen, die durch Bewegen von 2 Streichhölzern zur wahren führen. Z.B. zur Lösung 99-66=33 führen weit über 1000 falsche Gleichungen. Unter den veränderten Gleichungen gibt es auch einige wenige, die Wahr sind. Z.B. 39+47=86 ist die wahre Gleichung und zu dieser führen die wahren Gleichungen 133-47=86; 39+57=96 und 38+47=85. Da der Algorithmus alle wahren Gleichungen findet, kann jedes Rätsel damit gelöst werden.
Es wird untersucht, wie viele Streichhölzer entfernt und hinzugefügt wurden. Eine Streichholzbewegung ist daher einmal entfernen und einmal hinzufügen. Man kann also auch Rätsel lösen, die bei denen 2 Streichhölzer hinzugefügt werden müssen. Der Bruteforce-Algorithmus hat 9 ineinander greifende Schleifen, die jeweils die 9 (das erste Symbol ist ein Leerzeichen) verschiedenen Symbole mit 15 verschiedene Inhalte durchtesten. Das wären 15^9 Rechenschritte, was den Algorithmus unlösbar in PSpace verlegt. Um das berechenbar zu machen wird jede tiefere Schleife nur aufgerufen, wenn noch weniger als 3 Streichhölzer bewegt wurden. Ob das Rätsel damit in NP oder P liegt, weiß ich nicht, aber es ist mit nur 50000 Rechenschritte kein Problem für den Rechner die Lösung zu berechnen. Ich vermute, dass die Anzahl der Symbole Polyzeit benötigen und die Anzahl der bewegbaren Streichhölzer exponenziell viel Zeit brauchen.
Nimmt man 3 Stellige Zahlen, dann sind es 12 Symbole und damit 12 ineinander verschachtelte Schleifen 15^12. Bei 3 erlaubten Streichholzbewegungen sind es fast eine Million Rechenschritte und es gibt interessant viele Lösungen für wahre Gleichungen.
Gleichungen mit nur einem Streichholz sind rot und wahre Gleichungen sind grün. Neben den 10 Ziffern gibt es noch +, -, Leerzeichen, = und die 11. Der Bruteforce-Algorithmus findet auch die ganzen cleveren Lösungen, wo aus einer 0 eine 11 wird oder das linke Leerzeichen wird zum - oder zur 1.
Bitmaps
Fraktale... Addiere eine komplexe Zahl a, dann quadriere, dann addiere wieder a, dann quadriere. Wiederhole dies solange, bis der Betrag größer als 4 wird. Geht nicht?, dann Farbe = Weiß, sonst Farbe= Anzahl der Iterationen. Das Mandelbrot wird zu einem brennenden Schiff, wenn man nach dem Quadrieren ein Betrag gesetzt wird. Das kleine Schiff schwimmt etwa bei -1,75. Die Bilder sind Bitmaps und keine WMF-Datein. Anstelle meines billigen 50-Zeilers gibt es dafür das professionelle freie Programm "Kalles Fraktaler". Kalles Fraktaler nutzt eine Powerformel, die bei Deepzooms die lästige Wartezeit entfernt.
Geolandschaften als Bitmap. Würfel rollen über eine Matrix. Wo Sechsen sind, entstehen Hügel. Doppel und Dreiersechsen bringen viel Land.
WMF-Deckchin
Deckchin weicht! Das Makro habe ich nochmal neu geschrieben und kann mehr als sein Vorgänger. Wichtig war mir auch, dass die Deckchins auch wo anders erscheinen können und in einem beliebigen Winkel in beliebiger Größe erscheinen können. Damals waren Deckchins und Zipfelsterne möglich, die diese Entwicklungen haben konnten: Doppelrand, Kampf, Finsternis, Decolor, Deckwexel, Negativ, Weichi, Extraweichi, Verzipflungen und Schriftzug. Diese Entwicklungen sind durch Training und gewöhnliche Deckchinsteine erreichbar. Das neue Makro kann auch Deckchins zeichnen, die man nur durch den gefährlichen radioaktiven Mutationsstein bekommen kann. Somit gibt es Dreirand, Doppelrandkampf, doppelte Finsternis und Tricolor.
WMF-Deckchin füllt ein Rechteck mit Deckchins. Wenn eine Bitmap ausgewählt wird, dann wird diese durchdeckert. Die neue Grafik ahmt den Inhalt der Bitmap nach.
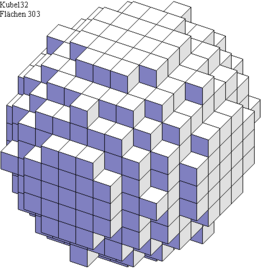
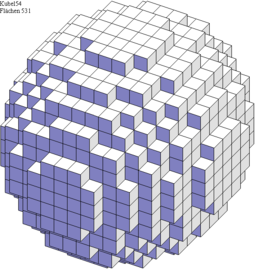
Kubel
Der Pythagoras als Kubel. Gewählt wird ein quadrierter Radius. Z.B. 32. Alle Voxel, die weniger oder gleich 32 vom Ursprung entfernt sind, werden angezeigt. Z.B. der Voxel mit der Entfernung (4;4;0) ist vorhanden, weil 4^2+4^2+0^2= 32. Zählt man den Radius schrittweise um 1 höher, dann vergrößert sich auch die Kubel schrittweise. Ist der Radius eine Quadratzahl, dann kommt nur ein Würfel hinzu.
Die große Kubel mit dem Quadratradius 1999 hat einen besseren Kompressionsalgorithmus, sodass verdecke Voxel nicht gezeichnet werden. Die Kreise auf der Kubel befinden sich in der Nähe kleinster Vektoren. So machen die Vektoren (1;0;0) und (0;1;0) und (0;0;1) die deutlichsten Kreise und (1;1;0) ist weniger deutlich.
Packer
Automatisch generierte Grafiken können in Massen produziert werden. Außerdem sollen sie möglichst groß sein. Große Grafiken haben jedoch ein hohes Datenvolumen. Dieses lässt sich mit verschiedenen Methoden packen.
- Layer: Objekte, die mit gleichen Füllern, Pinseln und Fonts gezeichnet werden, kommen auf dem selben Layer. Dadurch müssen die Malobjekte nicht gewexelt werden. Ein Wexel kostet je 4 Doppelbyte. Ist z.B. ein grünes Quadrat geometrisch neben einem roten Quadrat, dann sind beide Quadrate in der Datei weit auseinander.
- allgemeines Linienverbinden: Enden 2 Linien in einen Punkt, dann werden sie zu einer Polylinie. Das spart einen Punkt und ein Linien-Objekt. Eine Linie mit 2 Punkte benötigt 8 Doppelbyte - Eine Einsparung von 6 Byte.
- spezielle Eigenschaften des Kontext ausnutzen: Z.B. Statt 4 kleine Dreiecke kann man ein großes Dreieck mit einem kleinen Dreieck darin zeichnen, was 2 Dreiecke spart. Statt 3 Rechtecke nebeneinander kann man auch 2 Rechtecke übereinander zeichnen. Ist ein Polygon rechteckig, dann kann man auch ein Rechteck nehmen. Ein rechteckiges Polygon benötigt 12 Doppelbyte und ein Rechteck nur 7. Muster suchen: z.B. Rechtecke im Linienlabyrinth. Solche Muster haben meist ihre eigenen Malobjekte, was Farbe ins Spiel bringt.
Das Dateiformat ist weiterhin WMF und kann noch mit einem generischen Packer Zip, Rar oder 7z komprimiert werden.
Sonstige
Verschiedene Spiele. Skat, Würfel, Labyrinth, Liniengitter, 3D-Diagramme, Punktwolken sowie eine volle Ladung Querschnitte.