Kunst - Lateinmuster
Die Lateinmuster entdeckte ich im trockenen Lateinunterricht. Dort malte ich Pfeile, die an den Wänden abprallten. Dies ergibt ein schönes Muster.
Konstruktion eines Lateinmusters
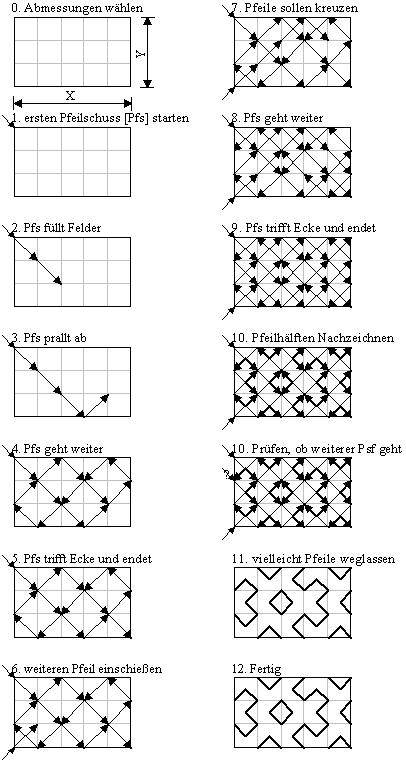
Zuerst startet man mit einem Rechteck auf karierten Papier, genauer einen Array. Oben links wird der erste Pfeil eingeschossen. Für den Pfeilschuss gelten folgende Regeln:
* Pfeilschuss ist die Richtung der einzelnen Pfeile
* Der Pfeilschuss verläuft diagonal und füllt jedes Kästchen mit einem Pfeil in seine Richtung
* Der Pfeilschussfüllt weitere Kästchen mit dem Pfeil in seine Richtung
* an den Wänden prallt der Pfeilschuss ab und ändert seine Richtung um 90°
* der Pfeilschuss endet, wenn er auf eine Ecke oder einen Pfeil in seine Richtung trifft
Ein Lateinmuster ist vollständig, wenn in jedem Kästchen 2 sich kreuzende Pfeile enthalten sind. Man muss mindestens 2 Pfeile einschießen.
Dieses Beispiel zeigt die Konstruktion eines Lateinmusters mit den Maßen 3x5
Anzahl der Lateinmuster
Ein Lateinmuster wird durch seine Abmessungen und der Richtungen der Pfeilschüsse definiert. Bei den Abmessungen ist der größte gemeinsame Teiler GgT sehr entscheidend.
Ist der GgT 1, dann gibt es genau 2 Lateinmuster und 2 Pfeilschüsse sind notwendig. Obenlinks wird immer eingeschossen, da das Variieren nur Symmetrien erzeugt.
Ist der GgT 2, dann gibt es einen weiteren Freiheitsgrad. Ein weiterer Pfeilschuss wird ein Kästchen neben dem ersten benötigt. Damit werden 3 Pfeilschüsse benötigt. Der erste ist obenlinks, der dritte ist oben links ein Kästchen daneben. Der zweite Pfeilschuss ist dort, wo noch Platz ist. Man weiß nicht genau, wo der erste Pfeil rauskommt. Es sind 4 Lateinmuster möglich. Von diesen sind aber immer 2 Stück eine Spiegelung eines anderen, sodass es 2 Muster bei 3 Schüsse sind.
Ist der GgT 3, dann wird ein weiterer Pfeilschuss benötigt, sodass es insgesamt 4 Schüsse sind. Der vierte Schuss ist neben den dritten. Die letzten 3 Pfeile dürfen in ihrer Richtung variiert werden, nur der erste ist vorgeschrieben. Damit sind 2^(4-1)=8 Muster möglich. Von diesen sind aber 4 gespiegelt.
Ist der GgT größer als 3, dann gilt
Pfeilschüsse = GgT+1
Lateinmuster = 2^(GgT-1)-2
Bei GgT = 4 sind es also 5 Schüsse und 6 Muster. Die -2 in der Formel kommt daher, dass sich der Pfeilblock mit dem gegenüberliegendem überlappt und 2 Muster identisch werden. Die Formeln gelten nicht für GgT < 4. Auch die Besonderheit von -2 gilt nicht für GgT = 3.
|
GgT |
Pfeile |
Muster |
|
1 |
2 |
2 |
|
2 |
3 |
2 |
|
3 |
4 |
4 |
|
4 |
5 |
6 |
|
5 |
6 |
14 |
|
6 |
7 |
30 |
Einfluss der Abmessungen
Eine weiteren Einfluss auf das Aussehen hat die Differenz der multiplizierten Abmessungen. Dabei werden die Abmessungen X und Y mit den Faktoren a und b multipliziert und der Differenzbetrag D gebildet. Das Paar a und b mit den kleinsten Differenzbetrag ist maßgebend.
D = Abs(a*X-b*Y)
Der einfachste Fall ist, wenn X und Y fast gleich groß sind. Damit ist GgT=1 und die Differenz ist auch 1 mit a=1 und b=1. Die Muster haben immer folgendes Aussehen:

Das linke Muster nenne ich Quadrat und das reche Dreieck. Dies sind die Grundmuster. Das Quadratmuster besteht aus 4 viertel Quadrate. Im Quadratmuster gehen alle Linien von einer Kante des Rechteckes zur anderen. Beim Dreieckmuster hingegen ist es nur eine Linie, die im Dreieck verläuft. Der Rest ist mit Karos aufgefüllt. Das Dreieckmuster ist das Grundelement eines jeden gefüllten Kästchens mit 2 Pfeilhälften.
Ist die eine Abmessung doppelt so groß, also z.B. Y= 2*X+1, dann ist GgT=1, die Differenz = 1 und a=1 und b=2. Die Muster haben immer folgendes Aussehen.

Das Aussehen ist mit dem vorherigen Identisch. Das Quadratmuster hat nun 4 Viertelquadrate und 2 halbe Quadrate, also 2 Quadrate. Das Dreieckmuster hat 2 Dreiecke. Der Verlauf der beiden Dreiecke ist das Lateinmuster 2x1.
Dies lässt sich verallgemeinern auf z.b Y= 3*X+1. Am Aussehen ändert sich wenig

Das Aussehen ändert sich im Detail, wenn die Differenz nicht mehr 1 ist. Z.B. die Differenz soll 2 sein. Bei fast gleich großen Abmessungen geht das mit Y=X+2. Da macht es einen Unterschied, ob GgT=1 oder GgT=2.
Bei GgT=1 sind beide Muster vom Typ Dreieck. Aus den Karos wurden teilweise Kreuze. Bei GgT=2 ist eines vom Typ Dreick und das andere ist vom Typ Quadrat. Das Dreieckmuster ist wie GgT=1 und beim Quadratmuster sind zwischen die Quadrate Karos aufgetaucht.

Lässt man die Abmessungen fast gleich groß, aber die Differenz bei 3, dann gibt es auch hier wieder den Unterschied zwischen GgT=3 oder GgT=1. GgT=2 ist nicht möglich. Bei GgT=1 gibt es ein Quadratmuster, bei den der Zwischenraum vollständig mit Karus aufgefüllt ist. Und es gibt ein Dreieckmuster, bei den sich die Karos zu Kreuze und kleine Quadrate weiterentwickelt haben. Bei GgT=3 gibt es 4 Lateinmuster. 2 davon ähneln GgT=1 und bei den anderen sind die Kreuze nicht zu Karos geworden, sondern zu Käsekästchen. Bei dem Quadratmuster sind nicht gleichmäßig Karos zwischen den Linien, sondern Karos und Kreuze gemischt.

Es lässt sich also eine Evolution der Karos ablesen. Je größer die Differenz ist, desto größere Objekte entstehen aus den Karos. Bei den Quadratmuster gibt es diese Entwicklung: Zwischen den Linien entstehen Karus, die dann anwachsen. Entweder sie wachsen gleichmäßig oder unterschiedlich. Bei den Dreieckmuster wächst im jeden Differenzschritt die Häfte der Karos. Bei der Entwicklung gibt es 2 Möglichkeiten: Vorwärtskopie oder seitliche Kopie. Wird ein Karo seitlich Kopiert oder vorwärts kopiert, dann entsteht ein Kreuz. Bei dem Kreuz gibt es unterschiedliche Entwicklungswege. Wird es vorwärts kopiert, dann wird aus ihm kein kleines Quadrat. Wird es seitwärts Kopiert, dann wird aus ihm ein Käsekästchen. Die nächste Entwicklungsstufe aus den beiden Varianten sind die 3 Fälle: mittleres Quadrat; Festung; großes Käsekästchen.
Also bisher wurde folgendes untersucht
* das Grundmuster Dreieck und Quadrat
* dass Dreieck und Quadrat erhalten bleiben, wenn eine Abmessung ein Vielfaches der anderen ist und GgT=1
* wie sich das Muster im Detail ändert, wenn die Differenz erhöht wird
* wie sich die Formen entwickeln, wenn die Differenz erhöht wird
Jetzt wird es eine Stufe komplizierter. Als Beispiel wird 25x33 verwendet. Die Differenz scheint 8 zu sein und die Evolution ist auch wie beschrieben.

Die Karos wurden zu große Quadrate oder zu große Käsekästchen. Das Muster gliedert sich nun in 3 Ebenen
1. Mustertyp: Quadrat oder Dreieck
2. Botschaft: 3x4
3. Detail: große Quadrate oder große Käsekästchen
Die Ebene Botschaft ist dazwischen hinzu gekommen. Die Konturen der großen Linien sehen aus wie das 3x4 Muster. Das große Käsekästchen bedeutet das Karo in 3x4 und die Verläufe der anderen Linien bilden den Rest von 3x4 nach. Die Zahlen 3 und 4 sind a und b, denn
D = Abs(a*X-b*Y)
D= Abs(4*25-3*33)= 1
Die Differenz ist also nicht 8, sondern 1. Ist die Differenz sehr klein, dann ist die Botschaft sehr klar. Die Botschaft des Musters lautet daher 3x4.
Wichtiges Detail: Beide Typen sind Dreieckmuster. Das mit den großen Quadraten sieht Quadratisch aus, aber rechts ist die Linie, die das kantige Dreieck bildet. Ist GgT=1, dann wird das Quadratmuster a*b nebeneinander gesetzt. Daraus entstehen die großen Quadrate aber der Mustertyp selbst kann von Quadrat zu Dreieck werden.
Erhöht man die Abmessungen auf 25x 34, dann
D = Abs(4*25-3*34)= 2

Die Botschaft ist schlechter erkennbar, weil die Differenz größer ist. Im Gegensatz zu 25x33 gibt es hier das Quadratmuster und das Dreieckmuster. Dadurch ist das Muster mit den großen Quadraten nicht wieder zu finden. Die Ebenen vom 25x33 sind
1. Muster: Quadrat oder Dreieck
2. Botschaft: 3x4
3. Detail Quadrat: Abstand von 7 zwischen den Linien und aufgefüllt mit Karos und Kreuze
3. Detail Dreieck: Verschwommene Linie der Botschaft und Zwischenraum aufgefüllt mit Karos und Kreuze.
Karos und Kreuze sind charakteristisch für eine Differenz von 2.
Ein anderes Beispiel ist 48x35.

Man kann die Botschaft 3x2 darin vermuten, denn
D = Abs(2x48-3*35)= 9
9 ist immerhin kleiner als 48-35= 13. Doch 9 ist sehr unscharf und im Muster ist was Klareres zu sehen. Nimmt man 8x11, dann
D = Abs(8x48-11*35)= 1
1 ist gegenüber 9 oder 13 maßgebend.
1. Muster: Quadrat
2. Botschaft: 8x11
3. Detail: Käsekästchen als Karos in der Botschaft. Rest aufgefüllt mit Karos
Eine Differenz von 1 hat nur Karos zum Auffüllen.
Zu guter letzt noch 46x36. Dieses Lateinmuster sieht sehr chaotisch aus. Es hat eine Differenz, die so groß ist, dass die Botschaft nicht erkennbar ist. Bemerkenswert ist, dass hier die Figuren zum Teil einfach symmetrisch sind und nicht wie bei den anderen doppelsymmetrisch.

Es lassen sich also diese Regeln für Lateinmuster festhalten:
- Ein Lateinmuster hat als Grundmuster Quadrat oder Dreieck
- GgT der Abmessungen bestimmt, wieviele Muster es für diese Abmessung gibt
- Es lässt sich in den 3 Ebenen Typ, Botschaft und Detail untergliedern
- Die Differenz bestimmt die Klarheit der Botschaft
- Die Differenz bestimmt das Detail
- D=1 hat im Detail nur Karos, D=2 hat auch Kreuze, D=3 hat kleine Quadrate oder Käsekästchen
- Die Botschaft ist die Abmessung eines kleineren Lateinmusters mit den Abmessungen a*b
- D = Abs(a*X-b*Y), wobei das Paar a und b so gewählt werden soll, dass D minimal wird
- Bei GgT=1 sind alle kleinen Formen Doppelsymmetrisch
- Bei GgT>1 sind alle Formen einfach symmetrisch. Der Formenreichtum nimmt bei hohem GgT zu

Farbliche Gestaltung
Für die Darstellung der Lateinmuster nehme ich natürlich das Dateiformat WMF, da ich ja nur noch auf fertige Malfunxionen zugreifen brauche.
Um die Datei zu packen hatte ich Linien verbunden. Dies ist notwendig, denn jede Linie braucht 16 Byte. Bei einem Muster 100x100 wären das 320 000 Byte. Die Dateigröße ist in VBA auf etwa 50MB begrenzt. Da ich möglichst viel in ein RTF haben will, lohnt es sich. In RTF benötigt jedes WMF-Byte doppelt so viel, also 640 000 Byte. Die beiden Linien lassen sich in jedem Kästchen einen, sodass 2*16= 1*20 wird. Werden jedoch Karos erkannt, dann 4*16= 2*20 = 1*24. Dies sind nur noch 3/8 der Ursprungsgröße. Dann lassen sich Kreuze erkennen mit 12*16= 6*20= 1*56 und noch generisch zusammenfassen.
Da Formen erkannt werden, lassen diese sich auch einfärben und auszählen. Diese Formen werden erkannt und eingefärbt:

Zuletzt noch ein Wort zur Entropie eines Lateinmusters. Die Muster 99x101 würden in RTF (100*100*(16*2)*2)*2= 1280 000 Byte benötigen. Durch packen kam ich auf etwa 300 000 Byte runter und zippen lässt 20 000 Byte übrig. Es sind also maximal 20 000 Byte an Information drin. Statt an Speicher zu denken, muss hier ein anderer Denkansatz gewählt werden:
Jedes Kästchen enthält 2 Pfeile, die diagonal nach links, rechts, oben oder unten zeigen. Es sind 4 Zustände für jedes Kästchen. Bei 4 Zustände werden 2 exakt Bit benötigt, denn log2(4)= 2. Damit haben die Muster insgesmmt (100*100*2)*2= 40 000 Bit Entropie. Durch die Pfeilregel ist ein Kästchen berechenbar, wenn Seine Nachbarn obenlinks und obenrechts bekannt sind, sodass (100+100)*2*2= 800 Bit. Die Regel, dass die Pfeile an den Wänden abprallen, lässt kaum noch Freiheitsgrade zu. Statt 800 Pfeile werden nut GgT+1 an Pfeilen benötigt. Dies sind etwa 4 Pfeile, also nur noch 2 Bit. Da zu den Mustern alle Varianten ausgegeben werden, ist keine weitere Information nötig (0 Bit). Die einzige Information, die nötig ist, sind die Abmessungen. Diese sind 2 ganze Zahlen, die sich mit je 2 Byte darstellen lassen.
Also von den 1280 000 Byte sind nur 4 Byte relevante Information, der Rest ist durch Berechnung vorhersagbar. Ein Lateinmuster besteht zu fast 100% aus Luft.
Lateinfragment
Lateinmuster lassen sich in kleinere Elemente zerlegen. Diese nenne ich Lateinfragment. Doch zuerst einmal beliebige Muster mit abnehmender Entropie.
Auf einem karierten Papier werden manche Linien am Kästchen nachgemalt. Malt man diese mit einer Wahrscheinlichkeit von 50% nach, dann entsteht ein chaotisches Muster.
Der Zufall ist nicht in der Lage Strukturen höherer Ordnung zu schaffen. Alles was in diesem Muster entstanden ist, sind Karos und ganz selten mal ein Kreuz. Höhere Objekte sind so unwahrscheinlich, dass man astronomisch große Flächen braucht um diese zu finden. Nach vielen Würfeln habe ich auch mal ein kleines Quadrat gesehen. Die Entropie dieses Musters ist sehr hoch, und zwar 1 Bit für jede Linie (nachgezeichnet oder nicht). Dies sind 2 Bit pro Kästchen. Für ein 100x49 Feld sind dies 9800 Bit.
Als erstes kann man die Freiheitsgrade jeder Linie einschränken. Jede Linie soll den entgegengesetzten Zustand haben, wie sein Vorgänger. Schaut man aufs ganze Papier, dann hat man durchgehend gestrichelte Linien horizontal und vertikal. Jede Zeile und Spalte kann nur noch 2 Zustände haben. Entweder sie beginnt mit einem Strich oder nicht. Die Entropie ist deutlich geringer, weil jede Zeile nicht mehr so viele Bits hat wie Spalten, sondern nur noch ein Bit. Für ein 100x49 Feld sind dies nur noch 149Bit.
Durch diese Einschränkung ist die Entropie stark gesunken und die Wahrscheinlichkeit auf höhere Strukturen drastisch erhöht. Häufig erscheinen primitive Formen wie Kreuze, Doppelkreuze und kleine Quadrate. In den Lateinmustern kommen diese zwar vor, aber das Muster sieht im Gegensatz zu den Lateinmustern noch sehr ungeordnet aus.
Lateinmuster haben periodische Strukturen. Eine Periode hat nur so viel Entropie, wie seine Länge an Bits. Bei den Lateinmustern gibt es neben der Regel, dass die Linien gestrichelt sind auch die weitere Regel, dass die Pfeile an den Wänden abprallen. Wie soll der Pfeil an einer Wand abprallen, die senkrecht ist? Diese Regel ist nicht umsetzbar und ein gleichwertiger Ersatz muss her. Dazu wird als erstes die Regel eingeführt, dass die Bits eine Periode haben müssen. Die Variable "Exponent" sagt, wie lang die Periode ist. Bei einem Exponent 10 gibt es 2^10 Möglichkeiten und die Entropie ist 10 Bit. Bei 10 Bit sind diese Muster möglich:
So wie es aussieht, sind in den 1024 Möglichkeiten auch Muster dabei, die in den Lateinmustern vorkommen. Jedoch sind dies deutlich weniger. Auffällig ist, dass grüne Doppelkreuze vorkommen, die man in einem Lateinmuster nur ab GgT7 findet. Viele der 1024 Muster sind jedoch doppelt. Diese kann man rausschmeißen und die Menge eingrenzen. Für das Eingrenzen gibt es 2 Regeln. Muster mit komplementären Bits sind gleich. Z.B. Nummer 782 = 241 oder in Bit 1100001110=0011110001. Zur Erinnerung: Jedes Bit steht dafür ob die Zeile mit einem Strich beginnt oder nicht. Durch die Komplementärregel gibt es nur noch halb so viele verschiedene Muster, sodass man sagen kann, dass jede Zahl mindestens so viele Nullen wie Einsen enthalten muss. Die zweite Regel ist die Shiftgleichheit. 2 Muster sind identisch, wenn die beiden letzten Bits nach vorne geschoben werden z.B. 1100001110= 1011000011. Dies darf man so oft machen, wie die Zahl lang ist. Bei Länge 10 also 10 mal. Jedoch kann man bei geraden Längen nur 5 verschiedene Zahlen erzeugen. Dennoch lassen sich die Möglichkeiten um den Faktor 5 reduzieren. Vorher 1024, komplementär 512, jetzt nur noch etwa 102,4. Warum aber 2 Bits schieben und nicht eins? Schiebt man ein Bit, dann wird das Muster komplementär. Manche komplementären Muster sind nicht gespiegelt, sondern verschieden. Um diese nicht zu verpassen, müssen 2 Bit gleichzeitig geschoben werden.
Dazu mal ein Beispiel. Es gibt die Zahl 000011 und dessen Komplement 111100. Der Exponent ist 6. x Bedeutet, dass das Lateinfragment aus Kreuze besteht und # bedeutet Käsekästchen. 000011 hat Kreuze und 111100 Käsekästchen. Kreuze sind keine Spiegelung der Käsekästchen, also ist das Komplement anders. Nun wird um ein Bit geschoben. 000110 hat Käsekästchen und 111001 nun Kreuze. Für alle Zahlen ergibt sich 000011x; 000110#; 001100x; 011000#; 110000x; 100001# und 111100#; 111001x; 110011#; 100111x; 001111#; 011110. Von 12 Zahlen brauchen nur 2 dargestellt werden, der Rest ist doppelt.
Die Lateinfragmente, die auch in den Lateinmustern vorkommen, müssen diese Bedingung erfüllen
Bitstring= "01" & Inv(x) & Xmod2 & X & "0"
Dabei sind
X = Nummer \ 2
Xmod2 = X mod 2
& verbindet 2 Texte z.B. 1+1= 2, aber 1&1 = 11
Inv(x) spiegelt und invertiert den Bitstring. Z.B. 0001 wird (zwischenschritt entweder 1000 oder 1110) zu 0111
Die Nummer ist die Nummer aus dem Lateinmuster. Die Anzahl der Lateinmuster berechnet sich mit der Formel 2^(GgT-1)-2. GgT-1 kann als neuer Exponent angesehen werden. Daraus folgt, dass der Bitstring doppelt so lang ist wie der Exponent. Für einen Bitstring der Länge 10 kommen nicht mehr 1024 Muster in Frage (oder 102,4), sondern nur noch 32. 32 hat den Exponent 5 bei GgT6. Die 32 sind die verschiedenen Möglichkeiten, wie man Pfeile einschießen kann. Somit hat das Feld 100x49 nur noch eine Entropie von 5 Bit. Im Gegensatz zu den Lateinmustern ist die Entropie von den Abmessungen unabhängig und stattdessen von der Länge des Bitstrings abhängig. So sehen einige Lateinfragmente aus:
Ein Lateinmuster setzt sich aus 2 komplementäre Lateinfragmente zusammen. Meist ist das Komplement eine Spiegelung und es sieht so aus, als wäre das Lateinmuster Identisch.
Mit dieser Exceltabelle lässt sich ein RTF mit vielen Lateinmustern oder Lateinfragmenten erstellen. Die Abmessungen sind frei wählbar. Ein Krampf war es, die langsamen Lateinfragmente schneller zu machen.
Lateinmuster.xlsb
xlsb Datei [118.9 KB]

